Introduction to the Davinci interface
Contents |
Starting the KRC function
To start the KRC function in davinci, simply run the krc() function:
% davinci dv> krc()
When started in this manner, the krc function will provide some context and definitions for some of the most common inputs
Simple Runs for Mars
Now let's run KRC for a simple case on Mars to determine the surface temperature in Gale Crater (latitude = -4.5; longitude = 137.4)
dv> out=krc(lat=-4.5,lon=137.5)
Read TEXT file: 61 lines
Found Default File: $DV_SCRIPT_FILES/krc_support/porb_defaults/Mars_Mars.porb.hdf
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/ti_map2ppd_v4.vicar: VICAR bsq image: 720x360x1, 32 bits
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/albedo_2ppd.vicar: VICAR bsq image: 720x360x1, 32 bits
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/mola_2ppd.vicar: VICAR bsq image: 720x360x1, 32 bits
Running KRC model with:
Output:
Every ~1.000 Ls (1.9083 JD) for 360 seasons starting at 0.10 Ls
For 96 times per day, every 15 local minutes
Running model WITH NO temperature prediction
because DELJUL < 3.0779
For a Surface With:
29 Layers with uniform material properties and 384 daily model time steps
and T-dependant material properties
and an insulating bottom edge condition
With Observation Parameters:
LATITUDE: -4.50 LONGITUDE: 137.50
ELEVATION: -3.606km^ SLOPE/AZIMUTH: 0.00/0.00deg
ALBEDO: 0.228^ OPACITY: 0.300
HOUR: All LS: All
Upper Material:
INERTIA: 230.00
CONDUCTIVITY: 0.0502*
DENSITY: 1770.00*
SPECIFIC HEAT: 595.55
POROSITY: 0.40
* = derived value unless overwritten by user
^ = from TES 2ppd map unless overwritten by user
& = ajusted for max authorized value
struct, 14 elements
tsurf: 96x1x360 array of double, bsq format [276,480 bytes]
tbol: 96x1x360 array of double, bsq format [276,480 bytes]
tatm: 96x1x360 array of double, bsq format [276,480 bytes]
down_ir: 96x1x360 array of double, bsq format [276,480 bytes]
down_vis: 96x1x360 array of double, bsq format [276,480 bytes]
time: 96x1x1 array of float, bsq format [384 bytes]
ls: 1x1x360 array of double, bsq format [2,880 bytes]
lat: -4.50000
elev: -3.60558
layer: struct, 8 elements
thickness: 28x2x1 array of double, bsq format [448 bytes]
center: 28x2x1 array of double, bsq format [448 bytes]
top: 28x2x1 array of double, bsq format [448 bytes]
center_mass: 28x1x1 array of double, bsq format [224 bytes]
mass_burden: 28x1x1 array of double, bsq format [224 bytes]
thermal_scales: 28x1x1 array of double, bsq format [224 bytes]
tmax: 28x1x360 array of double, bsq format [80,640 bytes]
tmin: 28x1x360 array of double, bsq format [80,640 bytes]
anc: struct, 11 elements
krccom: struct, 5 elements...
JDate: 1x1x360 array of double, bsq format [2,880 bytes]
ref_pressure: 1x1x360 array of double, bsq format [2,880 bytes]
taud: 1x1x360 array of double, bsq format [2,880 bytes]
total_frost: 1x1x360 array of double, bsq format [2,880 bytes]
avg_heat_flow: 1x1x360 array of double, bsq format [2,880 bytes]
frost_alb: 1x1x360 array of double, bsq format [2,880 bytes]
frost: 1x1x360 array of double, bsq format [2,880 bytes]
tatm_predict: 1x1x360 array of double, bsq format [2,880 bytes]
delta_t_rms: 1x1x360 array of double, bsq format [2,880 bytes]
converge_days: 1x1x360 array of double, bsq format [2,880 bytes]
version: "v3.2.1"
alb: 0.228235
body: "Mars"
The output is a structure containing various model parameters, as well a calculated quantities.
Surface temperatures are stored in .tsurf, local times in .time, and Ls in .ls Local times are stored in the x axis, depth in the y axis (not used yet), and season in the z axis.
So let's plot a diurnal temperature curve at Ls = 0.1 (first ls index):
dv> plot(out.tsurf[,1,1],xaxis=out.time) dv>
Let's plot a seasonal temperature curve at 0:25 (first time index):
dv> plot(out.tsurf[1,1,],xaxis=out.ls) dv>
When provided with the coordinates of a specific location on Mars, the krc() function reads some contextual information from external maps:
- the elevation: ELEVATION: -3.606km
- the albedo: ALBEDO : 0.228
Of course, these parameters can be set by the user:
dv> out=krc(lat=-4.5,lon=137.5,ALBEDO=0.22,ELEV=-4.5) dv>
Frequently, you will want to work with a specific Ls
dv> out=krc(lat=-4.5,lon=137.5,ls=122.45) dv>
More generally, any parameter listed in an input file can be used as an input; run krc() to see the list of variable names.
dv> out_1=krc(lat=-4.5,lon=137.5,ALBEDO=0.22,ELEV=-4.5,INERTIA=120.,SLOPE=12.,SLOAZI=45.,N24=36,SPEC_HEAT=600.,PTOTAL=610.) dv> out_2=krc(lat=-4.5,DUSTA=0.91,ARC2=0.6,TAURAT=0.201)
Make sure to read the helplist to familiarize yourself with the definition and range of inputs.
More Advanced Functionalities
In this section, a few more advanced functionality are presented.
- Time-Dependent Albedo
KRC can work with Ls dependent surface albedo values. The input format is a 2 column array, with Ls and albedo values along the y axis.
dv> ALBEDO_ARRAY dv> 2x12x1 array of float, bsq format [96 bytes] 0.00000 0.230000 30.0000 0.250000 60.0000 0.270000 90.0000 0.250000 120.000 0.230000 150.000 0.220000 180.000 0.220000 210.000 0.250000 240.000 0.230000 270.000 0.250000 300.000 0.270000 330.000 0.250000 dv> out_1=krc(lat=0.,INERTIA=45.,ALBEDO=ALBEDO_ARRAY,hour=4.5) dv> out_2=krc(lat=0.,INERTIA=45.,ALBEDO=0.24,hour=4.5) dv> plot(out_1.tsurf,"Variable Albedo",out_2.tsurf,"Fixed Albedo",Xaxis=out_1.ls) dv>
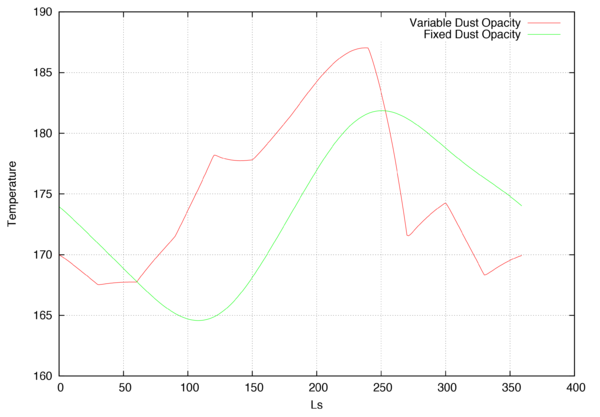
- Time-Dependent Opacity
dv> TAU_ARRAY 2x12x1 array of float, bsq format [96 bytes] 0.00000 0.310000 30.0000 0.320000 60.0000 0.400000 90.0000 0.600000 120.000 0.910000 150.000 0.720000 180.000 0.650000 210.000 0.600000 240.000 0.550000 270.000 0.200000 300.000 0.300000 330.000 0.230000 dv> out_1=krc(lat=0.,INERTIA=45.,TAUD=TAU_ARRAY,hour=4.5) dv> out_2=krc(lat=0.,INERTIA=45.,TAUD=0.4,hour=4.5) dv> plot(out_1.tsurf,"Variable Dust Opacity",out_2.tsurf,"Fixed Dust Opacity",Xaxis=out_1.ls) dv>
- Temperature-dependent Regolith Properties
KRC can work with temperature-dependent thermophysical properties (conductivity and specific heat, but not density). By default, temperature-dependent properties are turned on, but they can be turned off with LkofT="F"
dv> out_1=krc(lat=-4.5,INERTIA=200.,ls=0.,LkofT="T") dv> out_2=krc(lat=-4.5,INERTIA=200.,ls=0.,LkofT="F") dv> plot(out_1.tsurf,"I(T)",out_2.tsurf,"Fixed I",Xaxis=out_1.time)
When Temperature dependent properties are allowed (LkofT="T"), KRC expects 4 coefficients describing the conductivity and specific heat:
ConUp0,ConUp1,ConUp2,ConUp3 AND SphUp0,SphUp1,SphUp2,SphUp3
Refer to the helplist to see how these coefficients are used by KRC.
krc() can generate best guess coefficients for ConUp and SphUp based on the thermal inertia provided, assuming basaltic material.
These coefficients are generated by materials_krc(). Make sure to see how this function works to make sure the assumptions are OK for your application.
It is understood that the thermal inertia provided is at 220K (see helplist definitions)
dv> out=krc(lat=0.,INERTIA=700.,ls=356.,Mat1="basalt") dv> plot(out.tsurf,xaxis=out.time,"Basalt") dv>
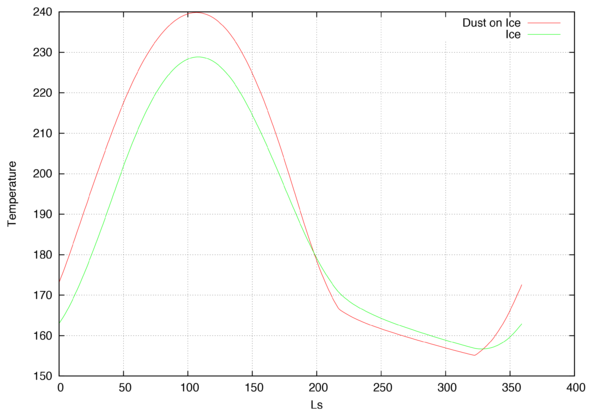
- Two layer Regolith
The interface can handle 2 layers of given thermophysical properties, but the latest version of KRC can be used to define n layers. A future release of the davinci interface will allow to run KRC from davinci with n layers. Be very patient.
To run 2 layers, the user must define:
- the upper and lower inertias (INERTIA, INERTIA2)
- the top material thickness in meters (thick)
evalN1_krc() is the function that links the number of mesh elements in each materials with thick and several numerical stability criteria.
Refer to evalN1_krc() for limits. Large inertia contrasts in conjunction with thin layers is typically not stable.
dv> out_1=krc(INERTIA=50,INERTIA2=2000,thick=5E-4,lat=75.,lon=0.,hour=12.) dv> out_2=krc(INERTIA=2000,lat=75.,lon=0.,hour=12.) dv> plot(out_1.tsurf[1,1,],"Dust on Ice",out_2.tsurf[1,1,],"Ice",Xaxis=out_1.ls) dv>
Simulated One Point Mode
KRC can run a one point mode, usually used to generate lookup tables to derive thermal inertia from a single temperature measurment.
The davinci interface to KRC includes a simulated one point mode, where the user feeds a temperature, and a thermal inertia value is retuned.
THIS SIMULATED MODE IS SIGNIFICANTLY SLOWER THAN THE ORIGINAL KRC ONE POINT MODE
In this mode, the full version of KRC is run for a number of cases (with thermal inertia being the only variable parameter), but an interpolation is used to derive a thermal inertia value.
To run KRC in this mode, amke sure to provide:
- a surface temperature: T
- a local time: hour
- a season: ls
dv> out=krc(lat=0.,lon=0.,T=179.23,hour=2.12,ls=67.)
Found Default File: $DV_SCRIPT_FILES/krc_support/porb_defaults/Mars_Mars.porb.hdf
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/ti_map2ppd_v4.vicar: VICAR bsq image: 720x360x1, 32 bits
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/albedo_2ppd.vicar: VICAR bsq image: 720x360x1, 32 bits
./Applications/davinci.app/Contents/Resources/library/script_files/krc_support/mola_2ppd.vicar: VICAR bsq image: 720x360x1, 32 bits
Running KRC model with:
Output:
Every ~8.000 Ls (15.2664 JD) for 45 seasons starting at 0.10 Ls
For 96 times per day, every 15 local minutes
Running model WITH temperature prediction for speed
For a Surface With:
29 Layers with uniform material properties and 384 daily model time steps
and T-dependant material properties
and an insulating bottom edge condition
With Observation Parameters:
LATITUDE: 0.00 LONGITUDE: 0.00
ELEVATION: -1.411km^ SLOPE/AZIMUTH: 0.00/0.00deg
ALBEDO: 0.186^ OPACITY: 0.300
HOUR: 2.12 LS: 67.00
Running One-Point Simulation Mode
Interpolating for TI values: 20.00 to 2200.00
with temperatures: 160.39K to 220.11K
from table indices: 1 to 40
134.793
dv>
In this example, the surface temperature T=179.23 K at the local time hour=2.12 (02:12AM) and season Ls=67.0 is found to be associated with a thermal inertia of 134.793 Jm-2K-1s-1/2.